Edisi Kedua (2019) buku “Kriptografi”

Alhamdulillah, pada bulan Juni 2019 yang lalu buku “Kriptografi, Edisi Kedua” saya sudah terbit. Buku Kriptografi, Edisi Kedua merupakan edisi baru dari buku sebelumnya yang berjudul sama. Buku ini disusun bagi siapapun (siswa, mahasiswa, umum) yang ingin mempelajari teknik-teknik di dalam kriptografi. Kriptografi merupakan kakas yang sangat penting dalam bidang keamanan informasi. Materi yang dibahas di dalam buku ini meliputi:
• Pengantar kriptografi
• Landasan matematika untuk kriptografi
• Algoritma kriptografi klasik
• Algoritma kriptografi modern
• Kriptanalisis sederhana
• Kriptografi kunci-publik
• Fungsi hash satu-arah
• Tanda-tangan digital
• Protokol kriptografi
• Pembangkit bilangan acak
• Elliptic Curve Cryptography
• Public Key Infrastructure (PKI)
• Manajemen kunci
• Steganografi dan watermarking
• Skema pembagian data rahasia (secret sharing scheme)
• Kriptografi visual (visual cryptography)
• Enkripsi homomorfik

Materi di dalam buku ini dilengkapi dengan kode program dalam Bahasa C++ (dan Matlab) yang mengimplementasikan beberapa algoritma. Diharapkan buku ini dapat memberikan pengetahuan kepada pembacanya tentang penggunaan kriptografi untuk keamanan pesan.

Tebal: 646 halaman
Penerbit: Informatika Bandung

Di bawah ini tulisan Prakata yang ada di dalam buku saya tersebut.

Prakata

Masalah keamanan informasi (information security) komputer menjadi isu penting pada era teknologi informasi saat ini. Banyak kejahatan cyber yang pernah kita dengar dari media massa. Pelaku kejahatan memanfaatkan celah keamanan yang ada di dalam sistem berbasis komputer untuk dimasuki dan melakukan manipulasi informasi.

Kriptografi merupakan ilmu yang berperan penting di dalam bidang keamanan informasi. Kriptografi digunakan untuk menjaga keamanan pesan atau informasi, baik informasi  yang ditransmisikan melalui saluran komunikasi maupun informasi disimpan di dalam media penyimpanan. Bahkan, kehidupan kita saat ini dilingkupi oleh kriptografi; mulai dari transaksi di mesin ATM, transaksi di dalam perdagangan elektronis (e-commerce),  transaksi dengan kartu kredit, percakapan melalui telepon genggam, mengakses internet, sampai mengaktifkan peluru kendali pun menggunakan kriptografi. Begitu pentingnya kriptografi untuk keamanan informasi, sehingga jika berbicara mengenai masalah keamanan yang berkaitan dengan penggunaan komputer, maka orang tidak bisa memisahkannya dengan kriptografi.

Buku Kriptografi edisi ke-2 ini disusun sebagai buku pegangan bagi mahasiswa yang mengambil mata kuliah kriptografi, jaringan komputer dan pengamanannya, atau kuliah lain yang terkait dengan masalah keamanan informasi. Kalangan umum yang ingin mempelajari kriptografi juga dapat menggunakan buku ini sebagai referensi.

Buku ini berawal dari dikat kuliah Kriptografi pada program Studi Teknik Informatika ITB. Diktat tersebut telah digunakan sejak tahun 2003, namun masih terpisah-pisah dalam bentuk lembaran handout kuliah. Pada Tahun 2004 semua handout kuliah disatukan menjadi sebuah diktat yang utuh, akhirnya diktat kuliah tersebut diterbitkan menjadi sebuah buku dengan materi yang lebih lengkap.

Sejak tahun 2018 yang lalu, Penulis mulai menyiapkan edisi kedua buku kriptografi. Buku edisi pertama sudah lama habis di pasaran. Sudah tidak terhitung banyak pihak yang menanyakan kapan buku kriptografi dicetak lagi. Penulis ingin memperbaiki materi di dalam buku dan menambahkan konten baru yang belum ada pada buku edisi pertama.

Buku Kriptografi edisi kedua disusun ke dalam 18 buah bab! Berikut penjelasan singkat masing-masing bab di dalam buku.

Bab 1 Pengantar Kriptografi. Bab ini memberikan gambaran umum kriptografi, asal mula dan sejarahnya, terminologi atau istilah-istilah yang terdapat di dalam kriptografi, perkembangannya mulai dari zaman kuno hingga zaman modern, dan kriptografi di Indonesia.

Bab 2 Landasan Matematika untuk Kriptografi. Bab ini menjelaskan secara ringkas dasar-dasar matematika yang diperlukan untuk mempelajari kriptografi. Dasar-dasar matematika yang terpenting di dalam kriptografi adalah teori bilangan (aritmetika modulo, kekongruenan, balikan modulo, bilangan prima, dan lain-lain) dan aljabar abstrak (teori grup, cincin, medan, dan Galois field). Bab 2 ini dapat dilompati jika pembaca sudah memiliki dasar-dasar matematika untuk kriptografi.

Bab 3 Serangan Terhadap Kriptografi. Bab ini membahas serangan-serangan (attack) yang dilakukan pihak lawan atau kriptanalis untuk menemukan kunci atau memecahkan cipherteks.

Bab 4 Kriptografi Klasik. Bab ini membahas algoritma enkripsi (cipher) zaman kuno hingga zaman sebelum ditemukannya komputer digital. Beberapa algoritma yang dibahas adalah Caesar Cipher, Vigenere Cipher, Playfair Cipher, Enigma Cipher, Affine Cipher, Hill Cipher, dan cipher transposisi. Selain itu juga dibahas pula kriptanalisis sederhana pada cipher-cipher tersebut sehingga dapat dipecahkan cipherteksnya.

Bab 5 Kriptografi Modern. Bab ini membahas konsep kriptografi pada era komputer digital. Kriptografi berkembang pesat sejak ditemukannya komputer digital. Konsep cipher alir (stream cipher) dan cipher blok (block cipher) menjadi bahasan utama di dalam bab ini.

Bab 6 Review Beberapa Cipher Alir dan Cipher Blok. Bab ini berisi ringkasan beberapa algoritma enkripsi berbasis cipher alir dan cipher blok. Semuanya adalah algoritma enkripsi dengan kunci yang sama untuk enkripsi dan dekripsi. Saat ini algoritma kriptografi kunci-simetri puluhan jumlahnya, tetapi kita tidak perlu mempelajari semuanya. Beberapa algoritma penting yang dibahas adalah RC4, A5, DES, GOST, 3DES, RC5, RC6, dan AES.

Bab 7 Kriptografi Kunci-Publik. Bab ini membahas konsep kriptografi kunci nirsimetri yang lebih dikenal dengan nama kriptografi kunci-publik. Beberapa algoritma kriptografi kunci-publik yang dibahas adalah RSA, ElGamal, Diffie-Hellman, dan Knapsack. Selain itu juga dibahas algoritma pengujian bilangan prima, karena bilangan prima banyak digunakan di dalam kriptografi kunci-publik.

Bab 8 Pembangkit Bilangan Acak. Bab ini membahas metode-metode untuk membangkitkan bilangan acak. Bilangan acak banyak dipakai sebagai parameter kunci di dalam algoritma enkripsi dan dekripsi.

Bab 9 Fungsi Hash. Bab ini membahas konsep fungsi hash untuk meringkas pesan berukuran sembarang menjadi pesan berukuran tetap. Beberapa algoritma hash yang dibahas adalah MD5, SHA-1, dan Keccak (SHA-3). Selain itu juga dibahas fungsi hash yang memakai kunci, yaitu MAC (Message Authentication Code).

Bab 10 Tanda-tangan Digital. Bab ini membahas konsep tanda-tangan dengan menggunakan algoritma kriptografi, yaitu tanda-tangan digital (digital signature).

Bab 11 Elliptic Curve Criptography. Bab ini membahas algoritma kriptografi kunci-publik yang menjadi primadona untuk perangkat mobile dan teknologi IoT (internet of things), yaitu kriptografi berbasis kurva eliptik (Elliptic Curve Criptography) atau ECC.

Bab 12 Infrastruktur Kunci Publik. Bab ini membahas konsep PKI (Public Key Infrastructure) yang mendukung penggunaan kriptografi kunci-publik. Di dalamnya juga dibahas sertifikat digital dan CA (Certificate Authority).

Bab 13 Protokol Kriptografi. Bab ini membahas konsep protokol komunikasi yang menggunakan algoritma kriptografi. Sebuah protokol yang populer untuk komunikasi antara client dan server juga dibahas yaitu protokol Secure Socket Layer (SSL).

Bab 14 Manajemen Kunci. Bab ini membahas daur hidup kunci, mulai dari pembangkitan, penyimpanan, distribusi, hingga penghancurannya.

Bab 15 hingga Bab 18 adalah materi tambahan (opsional) yang masih berkaitan erat dengan kriptografi. Bab ini memperkaya pengetahuan kita tentang keamanan informasi.

Bab 15 Steganografi dan Watermarking. Bab ini membahas teknik-teknik untuk menyembunyikan pesan di dalam sebuah media cover. Media cover yang umum digunakan adalah gambar (image). Dibahas pula penerapan steganogafi yang disebut watermarking.

Bab 16 Skema Pembagian Rahasia. Bab ini membahas teknik-teknik untuk membagi informasi rahasia (secret) menjadi sejumlah share kepada sejumlah partisipan, termasuk teknik untuk merekonstruksi secret berdasarkan suatu nilai ambang (threshold).

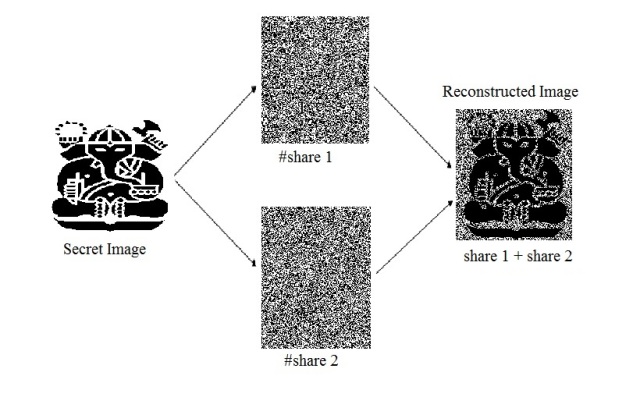
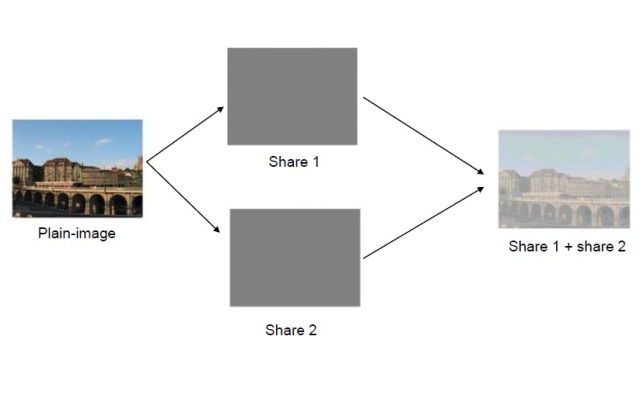
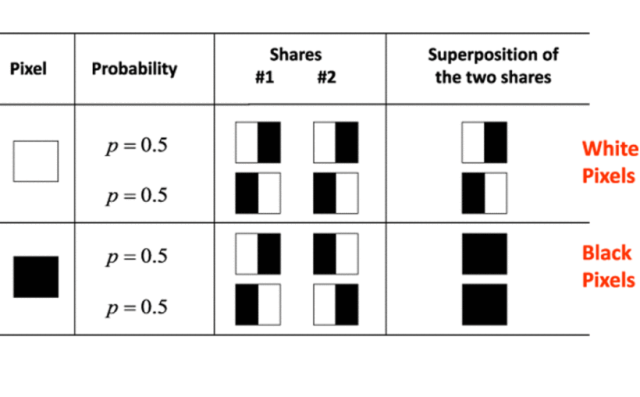
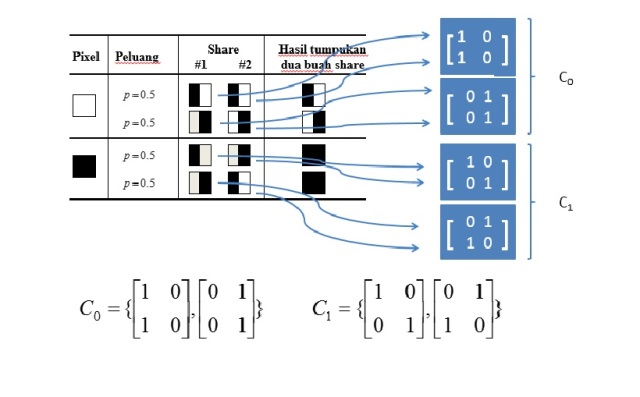
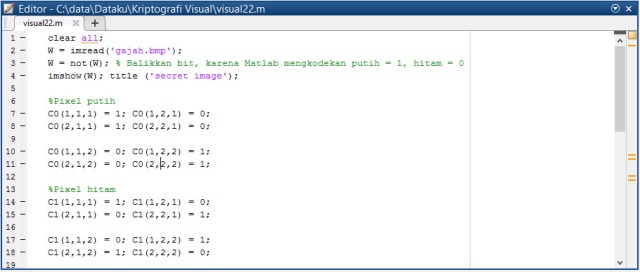
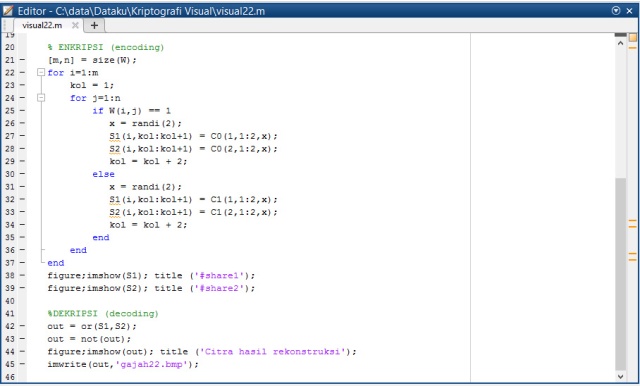
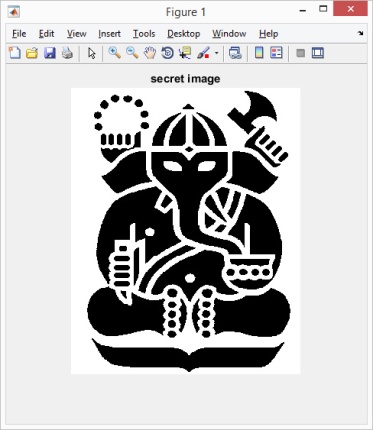
Bab 17 Kriptografi Visual. Bab ini membahas konsep enkripsi untuk informasi visual seperti gambar. Seperti halnya secret, gambar dapat dibagi menjadi sejumlah share kepada sejumlah partisipan, dan share-share itu dapat direkonstruksi kembali menjadi informasi yang dipersepsi secara visual.

Bab 18 Enkripsi Homomorfik. Bab ini membahas konsep komputasi pada cipherteks sedemikian sehingga hasil komputasi pada cipherteks bila didekripsi sama dengan hasil komputsi yang sama pada plainteksnya.

Bahan yang ada di dalam buku ini kebanyakan bersumber dari berbagai referensi yang disebutkan di dalam Daftar Pustaka. Sebagian lagi berasal dari pengalaman mengajar mata kuliah Kriptografi di teknik Informatika ITB. Buku ini dilengkapi dengan beberapa kode program dalam Bahasa C++ dan Matlab yang mengimplementasikan beberapa algoritma yang dibahas.

Untuk bisa memahami buku ini, pembaca dianjurkan sudah memiliki prasyarat matematika diskrit. Jika belum, maka di dalam Bab 2 diberikan review singkat. Prasyarat algoritma dan pemrograman juga diperlukan jika algoritma kriptografi ingin diimplementasikan menjadi program komputer.

Penulis juga mempunyai sebuah blog di WordPress yang membahas kriptografi, meskipun tidak sering di-update, silakan baca di  https://catatankriptografi.wordpress.com/

Akhirul kalam, semoga buku ini dapat memberikan pencerahan bagi pembacanya mengenai kriptografi.

Bandung, Maret 2019

Rinaldi Munir

Program Kriptografi Visual dengan Skema (2, 2) dan Ekspansi 4-subpixel

Kita lanjutkan program kriptografi visual untuk skema (2, 2). Jika pada tulisan sebelumnya setiap pixel (hitam atau putih) diekspansi menjadi dua (m = 2) buah sub-pixel , maka sekarang setiap pixel diekspansi menjadi empat (m = 4) buah sub-pixel. Skema pembagiannya ditunjukkan pada Gambar 1.

Gambar 1. Skema (2,2) dengan m = 4. (Sumber: Das,S., Nath, A., Samanta A., et all, “A Secure Approach for Data Hiding using Visual Cryptography”, International Journal of Innovative Research in Computer and Communication Engineering, Vol. 4, June 2016

Berdasarkan Gambar 1 di atas, kita dapat membentuk himpunan C0 dan C1 yang berisi semua matriks yang merepresentasikan share 1 dan share 1 untuk setiap pixel hitam dan pixel putih. Perhatikan Gambar 2.

Gambar 2. Himpunan C0 dan C1 yang berisi kumpulan matriks yang merepresentasikan share 1 dan share 2 dari pixel putih dan pixel hitam,

Kode program Matlab (release 2016) untuk mengenkripsi dan dekripsi citra biner dengan skema (2,2) dan m = 4 diperlihatkan di bawah ini.

Hasil run program Matlab di atas untuk citra kendang.bmp diperlihatkan pada gambar di bawah ini. Perhatikan bahwa ukuran share menjadi dua kali ukuran citra semula, baik tinggi maupun lebar. Hal ini karena setiap pixel diekspansi menjadi dua pixel dalam arah lebar dan dua pixel dalam arah tinggi.

Semoga bermanfaat!

Program Kriptografi Visual dengan Skema (2, 2) untuk Citra Biner

Selain kriptografi konvensional yang sudah kita kenal, terdapat satu jenis kriptografi lain yang menarik perhatian para ilmuwan keamanan data, yaitu kriptografi visual (visual cryptography).  Kriptografi visual mengenkripsi informasi dalam bentuk visual (teks yang dicetak, gambar, tulisan tangan) dengan cara membaginya menjadi beberapa buah transparansi (share). Untuk mendekripsinya sama sekali tidak dibutuhkan komputasi, tetapi cukup dengan menumpuk beberapa buah transparansi dan informasi yang ditampilkan dipersepsi secara visual.

Ide kriptograi visual pertama kali dikemukakan oleh Moni Naor dan Adi Shamir di dalam makalahnya berjudul Visual Cryptography (unduh di sini) yang dimuat di dalam jurnal EuroCrypt’94. Pada kasus sederhana, sebuah citra rahasia dibagi menjadi dua buah share, dan untuk merekonstruksi citra semula, kedua buah share tersebut ditumpuk bersama-sama (lihat Gambar). Citra hasil rekonstruksi yang dihasilkan memang tidak tepat sama dengan citra semula, tetapi itu tidak terlalu penting, yang penting informasi yang ditampilkan masih dapat dipersepsi atau dibaca secara visual. Anda masih bisa melihat gajah Ganesha pada citra hasil rekonstruksi tersebut, bukan?

Gambar 1. Kriptografi visual terhadap citra ganesha.bmp

Kriptografi visual dapat diterapkan baik untuk citra hitam-putih, citra grayscale, maupun citra berwarna (color images). Gambar 2 adalah contoh kriptografi visual untuk citra berwarna.

Gambar 3. Kriptografi visual untuk citra berwarna

Skema pembagian citra menjadi beberapa buah share disebut the secret image sharing scheme. Pada awalnya, Naor dan Shamir menerapkan skema kriptografi visual pada citra biner saja (citra hitam-putih). Skema yang paling sederhana adalah skema (2, 2), artinya citra dibagi menjadi dua buah share, dan untuk merekonstruksi citra kedua share tersebut ditumpuk bersama. Di dalam skema (2, 2), setiap pixel dibagi menjadi dua buah sub-pixel untuk setiap share.  Pixel putih dibagi menjadi dua kemungkinan pasangan sub-pixel dengan peluang 0.5, begitu pula untuk pixel hitam (lihat Gambar 3). Penumpukan kedua buah share dari pixel putih tidak menghasilkan tepat pixel putih semula, tetapi berupa campuran sub-pixel hitam dan sub-pixel putih. Karena itulah kita melihat cira hasil rekonstruksi terlihat mengandung noise. Sebaliknya, penumpukan dua buah share dari pixel hitam akan menghasilkan tepat pixel hitam semula.

Gambar 3. Ilustrasi skema (2, 2). Sumber: Ross, A., Visual Cryptography for Biometric Privacy, IEEE Transaction on Information Forensics and Security, Vol. 6, No. 1, March 2011.

Skema (2, 2) di atas diformulasikan dengan matriks sebagai berikut. Didefinisikan dua buah matriks C0 dan C1.  C0 adalah himpunan yang berisi semua matriks S yang merepresentasikan pixel putih.  C1 adalah himpunan yang berisi semua matriks S yang merepresentasikan pixel hitam. Pada hakekatnya C0 maupun C1 berisi semua matriks hasil permutasi kolom dari sebuah matriks. Pixel hitam dinyatakan sebagai nilai 1, sedangkan pixel putih bernilai 0.  Gambar 4 memperlihatkan himpunan C0 dan C1 untuk skema (2, 2).

Gambar 4. Himpunan C0 dan C1 berisi semua matriks kemungkinan share untuk ekspansi pixel hitam dan pixel putih.

Algoritma enkripsi (membagi gambar menjadi dua share) pada skema (2, 2) adalah sebagai berikut:

1.  Ambil sebuah pixel dari citra rahasia (plain-image), misalkan pixel P

2.  Jika P berwarna putih, ambil secara acak sebuah matriks S pada C0. Jika P berwarna hitam, ambil secara acak sebuah matriks S pada C1.

3. Misalkan P berwarna hitam dan matriks yang diambil dari C1 adalah sebagai berikut: S = [1  0; 0  1], maka share 1 adalah baris 1 dari S dan share 2 adalah baris 2 dari S. Jadi,
share 1 = [1  0] dan  share 2 = [0  1].

4. Ulangi langkah 2 dan 3 untuk pixel-pixel lainnya

Untuk melakukan dekripsi, kita cukup menumpukkan share 1 dan share 2. Penumpukan dua atau lebih share dapat dipandang sebagai operasi “OR” untuk setiap pixel pada posis bersuaian (lihat Gambar 5).

Gambar 5. Penumpukan dua buah share dapat dipandang sebagai operasi OR

Di bawah ini saya tampilkan kode program kriptografi visual untuk skema (2,2). Kode program ditulis dengan kakas Matlab 2016. Program menerima input citra biner (yang akan dienkripsi). Luaran program adalah dua buah citra share dan citra hasil rekonstruksinya.

Hasil running program untuk citra gajah.bmp adalah sebagai berikut (citra semula, share 1, share 2, dan citra hasil rekonstruksi):

Perhatikan, karena sebuah pixel diekpansi menjadi dua buah sub-pixel, maka citra hasil rekonstruksi memiliki lebar ukuran dua kali ukuran citra semula.

Eksperimen Steganalisis dengan Metode Visual Attack pada Citra Hasil EzStego Berformat GIF

Pengantar: Tulisan ini merupakan makalah yang telah dipresentasikan pada konferensi nasional SNATI (Seminar Nasional dan Aplikasi Teknologi Informasi) 2016 yang diselenggarakan oleh Jurusan Teknik Informatika, Universitas Islam Indonesia, Yogyakarta, pada tangal 6 Agustus 2016.

Makalah dalam format pdf dapat diunduh dari pranala ini.

~~~~~~~~~~~~

 

Algoritma EzStego, Algoritma Steganografi pada Citra GIF

Kebanyakan paper atau riset tentang algoritma steganografi diterapkan pada citra berformat bitmap (BMP) dengan memodifikasi bit LSB pixel secara langsung. Tidak terlalu banyak paper yang membahas algoritma steganografi pada format citra lain, misalnya JPEG atau GIF. Citra dengan format BMP sederhana, karena ia tidak dikompresi, sehingga setiap pixel menyatakan nilai keabuan secara langsung.

Sayangnya citra BMP sangat jarang digunakan di dalam World Wide Web karena ukuran memorinya yang besar.  Citra BMP tidak menjadi standard representasi citra untuk berbagai aplikasi, termasuk di Internet. Citra yang umum digunakan di dalam komunikasi dan  berbagai aplikasi adalah citra terkompresi seperti citra JPEG, GIF, PNG, dan lain-lain.

Tidak banyak paper tentang algoritma steganografi pada citra terkompresi. Tulisan ini membahas algoritma steganografi pada citra GIF.

Citra GIF

Citra GIF adalah jenis citra terindeks (indexed image) yang pertama kali diperkenalkan oleh Compuserve pada tahun 1987. Format GIF biasanya digunakan untuk menyimpan citra grafika komputer, citra ikonik, kartun, logo, animasi, maupun citra natural. Sebuah citra GIF terdiri dari sebuah palet warna dengan komponen Red, Green, dan Blue atau RGB, dan sebuah matriks pixel yang berisi indeks ke sebuah baris di palet. Dengan kata lain, nilai pixel pada matriks menyatakan indeks ke palet. Warna pixel ditentukan oleh kombinasi R, G, dan B pada baris palet yang diacu.

Struktur citra GIF (Sumber: Matlab)

Gambar 1 memperlihatkan struktur citra GIF. Di dalam gambar tersebut nilai 5 menyatakan elemen palet pada baris kelima. Pada baris tersebut,  R = 0.2902, G = 0.0627, B = 0.0627. Jadi, persepsi warna pada pixel 5 adalah kombinasi wana RGB. Karena kedalaman warnanya hanya sampai 256 buah saja, maka citra GIF cocok untuk gambar grafik buatan manusia seperti kartun, animasi, dan gambar-gambar menarik lainnya yang dibuat menggunakan kakas seperti Corel Draw, Photoshop, dan lain-lain.

EzStego

Salah satu algoritma steganografi yang cukup sederhana pada citra GIF adalah EStego. EzStego dikembangkan oleh Romana Machado (http://www.jjtc.com/Steganography/tools.html)  pada tahun 1996.

Algoitma EzStego menyisipkan bit-bit pesan dengan metode LSB.  Bit LSB dari nilai pixel (yang menunjuk ke nomor entri pada palet) diganti dengan bit pesan. Akibat penyisipan tersebut, nilai pixel dapat bertambah satu,  tetap, atau berkurang satu. Namun, karena nilai pixel merupakan pointer ke palet warna, maka nilai pixel yang baru (setelah penyisipan LSB) akan menunjuk ke warna berikutnya (atau ke warna sebelumnya) di palet yang tentu saja secara visual berbeda signifikan. Hal ini tentu menimbulkan degradasi warna yang membuat citra stego menjadi rusak.

Untuk meminimalkan degradasi warna, maka langkah pertama di dalam algoritma EzStego adalah mengurutkan warna-warna di dalam palet sedemikian sehingga perbedaan dua warna yang bertetangga adalah minimal. Perbedaan dua warna dapat dihitung dengan rumus jarak Euclidean. Misalkan warna 1 dinyatakan sebagai vektor (R₁, G₁, B₁) dan warna 2 dinyatakan sebagai (R₂, G₂, dan B₂). Jarak Euclidean kedua warna tersebut dihitung dengan rumus:

Jadi, proses pengurutan palet dilakukan dengan menghitung jarak antar warna di dalam palet, lalu mengurutkan palet berdasarkan jarak terkecil sedemikian sehingga akhirnya dua warna bertetangga memiliki jarak Euclidean yang kecil. Bit-bit pesan disisipkan pada bit LSB indeks dari palet yang terurut secara sekuensial.

Gambar 2 memperlihatkan ilustrasi penyisipan pesan di dalam EzStego. Misalkan terdapat delapan palet  yang berbeda warna. Angka 0-7 menyatakan nilai pixel di dalam  citra GIF. Misalkan kita ingin menyisipkan bit pesan  pada pixel bernilai 7. Warna pixel 7 pada citra asal adalah pada  indeks 4 (=100)  pada palet yang sudah terurut, dan warna pixel 3 adalah pada indeks 5 (=101) pada palet terurut. Kedua warna ini bertetangga dan sukar dibedakan. Jika kita menyisipkan bit “1” pada pixel 7, maka warnanya diganti menjadi indeks 3 pada palet terurut (100 –> 101).  Karena perbedaan warna antara dua warna bertetangga sangat kecil, perubahan tersebut  hampir tidak bisa dilihat oleh mata.

Ilustrasi proses penyisipan pesan di dalam EzStego (Sumber: A. Westfeld and A. Pfitzmann (1999). “Attack on Steganographic System”, Lecture Notes in Computer Sciences, vol. 1768, pp. 61-76)

Ekstraksi pesan  sangat mudah dilakukan. Sebelum proses ekstraksi, palet warna diurutkan sedemikian sehingga perbedaan dua warna yang bertetangga adalah minimal. Selanjutnya bit pesan  diekstraksi dari LSB indeks palet.  Kelemahan algoritma EzStego adalah tidak membutuhkan kunci sehingga kurang aman untuk penyembunyian pesan, sehingga siapapun yang mengetahui algoritmanya dapat mengekstrak pesan.

Ringkasan algoritma EzStego adalah sebagai berikut:

Embedding Algorithm

1. Urutkan palet dari citra cover (original image) berdasarkan jarak Euclidean
2. Assign indeks baru pda palet yang terurut dengan penomoran 0, 1, 2, … dst.
3. Ganti LSB dari indeks palet yang terurut dengan dengan bit-bit pesan.
4. Hasilnya adalah sebuah citra stego (stego-image).

Extraction Algorithm

1. Urutkan palet dari citra stego berdasarkan jarak Eucliedean.
2. Assign indeks baru pda palet yang terurut dengan penomoran 0, 1, 2, … dst.
3. Ekstraksi bit LSB dari indeks palet yang terurut.

Di bawah ini beberapa contoh gambar GIF yang disisipi pesan dengan algoritma EzStego. Program dibuat menggunakan kakas Matlab. Pesan yang disisipkan ke dalam citra adalah pesan teks, namun pesan dengan format lainnya pun tetap dapat disisipkan. Anda dapat melihat tidak terdapat degradasi warna pada citra stego.

Di bawah ini potongan program untuk mengurutkan palet:

 

Stegosploit: Penerapan Steganografi untuk Meng-hack Komputer

Steganografi adalah ilmu dan seni untuk menyembunyikan pesan rahasia di dalam sebuah media pembawa (carrier). Media pembawa saat ini sudah berupa digital, sehingga steganografi digital umumnya menggunakan media digital seperti citra (image), teks, video, dan audio.Penyisipan pesan ke dalam media pembawa tidak membuat kualitas media pembawa itu mengalami distorsi. Media yang telah disisipi pesan hampir tidak dapat dibedakan secara persepsi inderawi (visual atau audial) dengan media aslinya (cover). Inilah keunggulan steganografi dibandingkan kriptografi. Kriptografi menghasilkan cipherteks yang dapat menimbulkan kecurigaan (conspicious) bagi pengamat, sedangkan steganografi menghasilkan pesan yang tidak dapat dideteksi keberadaannya sehingga tidak menimbulkan kecurigaan (non-conspicious). Kriptografi menyembunyikan subtansi pesan, sedangkan steganografi menyembunyikan eksistensi pesan itu sendiri.

Meskipun steganografi merupakan salah satu teknik untuk mengamankan pesan rahasia, namun steganografi bukanlah pengganti kriptografi. Stegaonografi merupakan pelengkap kriptografi. Kriptografi dan steganografi digunakan secara paralel. Pesan rahasia dienkripsi terlebih dahulu (dengan suatu algoritma kriptografi) sebelum disisipkan ke dalam media pembawa. Silakan membaca review singkat tentang steanografi pada laman Wikipedia ini.

Steganografi yang populer adalah penyembunyian pesan di dalam gambar (image). Anda dapat menyisipkan pesan apapun di alam sebuah gambar, baik pesan dalam bentuk teks,  audio,  atau gambar sekalipun. Pesan dinyatakan di dalam bentuk bit biner. Di dalam ranah spasial (spatial domain), bit-bit pesan disisipkan ke dalam pixel, sedangkan di dalam ranah transform, bit-bit pesan disisipkan pada koefisien-koefisien hasil transformasi. Citra asli yang digunakan sebagai wadah penyisipan pesan disebut cover image, sedangkan citra yang sudah disisipi pesan disebut stego image. Antara cover image dan stego image sulit dibedakan secara visual (lihat gambar di bawah). Penerima citra stego mengekstraksi pesan yang tersembunyi di dalamnya menggunakan kunci rahasia tertentu. 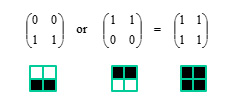Selama ini orang beranggapan steganografi hanya sekedar menyisipkan pesan rahasia semata, lalu sesudah itu selesai. Steganografi ternyata dapat digunakan untuk tujuan yang lebih jauh, salah satunya untuk meng-hack komputer. Selama ini  hacker melakukan hacking dengan mencari celah masuk ke dalam jaringan komputer target, atau menyusupkan kode program melalui attachment file dalam format PDF. Tetapi, ada cara lain yang tidak menimbulkan kecurigaan, yaitu melalui gambar-gambar. Adalah Saumil Shah, seorang peneliti keamanan dari India yang menemukan teknik hacking yang bernama Stegosploit. Seperti ditulis di dalam artikel berikut: How to Hack a Computer Using Just an Image, Shah mengatakan:

“I don’t need to host a blog,” Shah told Motherboard, “I don’t need to host a website at all. I don’t even need to register a domain. I can [just] take an image, upload it somewhere and if I just point you toward that image, and you load this image in a browser, it will detonate.“

Stegosploit menggunakan teknik steganografi untuk menyembunyikan malicious code (atau diistilahkan Shah sebagai exploit) di dalam sebuah gambar (format JPG atau PNG). Malicious code adalah kode program “jahat” yang ditulis dalam bahasa JavaScript . Kode program ini isinya perintah-perintah untuk membaca dan mengirimkan data dari komputer target ke penyerang. Jadi, dalam hal ini pesan rahasia yang akan disembunyikan adalah berupa teks kode program yang kemudian disisipkan pada pixel-pixel gambar. Gambar yang sudah disisipi malicious code ini tampak innocent sehingga tidak menimbulkan kecurigaan bagi penerimanya.

Gambar kucing ini mungkin tampak ‘cute’, namun sebenarnya di dalam gambar ini terdapat malicious code yang berbahaya

Setelah sebuah gambar disisipi malicious code, maka cara penyebarannya bisa menggunakan dua cara. Pertama, gambar (stego image) ditaruh pada sebuah laman web dengan perintah kepada pembaca untuk mengklik gambar tersebut (mungkin supaya tampil dalam ukuran yang lebih besar). Cara kedua, komputer target dikirimi surel (email) yang di dalamnya ada tautan (link) ke laman web yang berisi gambar tersebut.  Ketika pengguna meng-klik gambar tersebut sehingga tampil pada laman browser, maka malicious code di dalamnya diekstraksi (decoded) dengan elemen kanvas HTML 5  yang  berisi script untuk melakukan rendering citra. Ingatlah bahwa Stegosploit hanya bisa bekerja jika gambar dibuka di dalam browser, jadi jika gambar dibuka di dalam aplikasi photo viewer atau semacam Photoshop, ia tidak akan bekerja. 

Sekali malicious code berhasil di-ekstraksi dari gambar tadi, maka mulailah dia beraksi. Shah mendemokan cara Stegosploit bekerja. Ketika gambar di-klik, CPU menunjukkan penggunaan 100%, yang mengindikasikan malicious code berhasil bekerja. Malicious code membaca data dari komputer target lalu mengirimkannya kembali ke penyerang, tak lupa menampilkan pesan di layar: “You are hacked!“. Shah juga memprogram malicious code untuk melakukan tugas-tugas lain seperti mengunduh dan meng-instal spyware ke komputer target.

Moral dari Stegosploit yang ditemukan Shah adalah: berhati-hatilah jika anda suatu hari menerima kiriman gambar dari sumber yang tidak dapat dipercaya, jangan langsung di-klik., seperti contoh (ini hanya contoh saja) di bawah ini:

Sebuah surel yang berisi gambar yang siap untuk di-klik

Gambar yang tampak keren atau innocent bisa jadi mengandung program jahat yang akan meng-hack komputer anda. Waspada!

Kriptografi di Korea

Tahun lalu saya dan teman-teman di STEI mendapat kesempatan pelatihan cyber security ke Korea Selatan. Kami banyak mendapat pengalaman perkembangan cyber security di Korea. FYI, Korea Selatan adalah negara yang sangat maju dalam bidang keamanan informasi, termasuk bidang keamanan saiber. Hal ini bisa dimaklumi karena Korea Selatan memiliki musuh bebuyutan yang tidak pernah akur sampai sekarang, yaitu negara tetangga mereka sendiri, Korea Utara. Karena itu, rakyat dan Pemerintah Korea Selatan berusaha memproteksi dirinya dari berbagai usaha serangan saiber dari musuhnya itu, salah satunya melindungi data dan informasi rahasia mereka menggunakan kriptografi. Tulisan ini hanya akan membahas tentang kriptografi di Korea.

Pernah mendengar algoritma kriptografi bernama SEED? SEED adalah sebuah block cipher yang terkenal dari Korea. SEED dikembangkan oleh KISA (Korea Internet and Security Agency), yaitu sebuah badan yang menangani insiden terkait keamanan informasi atau CERT (Computer Emergency Response Team), dan sekarang perannya diperluas untuk menangani kebijakan dalam bidang Internet. SEED digunakan secara luas oleh industri di Korea, tetapi jarang ditemukan di luar Korea.

Di Korea kebijakan yang terkait penggunaan kriptografi sangat ketat. Mereka mempunyai aturan yang hirarkhi seperti yang tergambar pada diagram Venn di bawah ini.

Semua algoritma kriptografi yang akan diimplementasikan di dalam produk harus lulus uji program validasi algoritma kriptografi yang disebut CAVP (Cryptographic Algorithm Validation Program). Sekanjutnya, jika sudah lulus, maka modul yang menggunakan algoritma tersebut diuji dan divalidasi oleh K-CMVP (Korea Cryptographic Module Validation Program). Yang dimaksud dengan modul adalah perangkat lunak maupun perangkat keras yang memakai algoritma tersebut. K-CMVP sendiri pada awalnya dibentuk oleh NIST (National Institute of Standard and Technology) –sebuah lembaga standard dari Amerika– dan CSEC (Communications Security Establishment Canada), pada tahun 1995. Semua modul kriptografi yang digunakan oleh Pemerintah Korea untuk melindungi informasi rahasia melalui program validasi K-CMVP ini.

Setelah melewati uji validasi K-CMVP, maka semua fungsi keamanan dari produk IT (H/W maupun S/W) yang diimplentasikan di dalam produk security, dievaluasi oleh CC (Common Criteria). CC adalah standard internasional yang mengevaluasi dan mensertifikasi produk IT untuk memastikan apakah sudah diimplementasikan dengan benar dan sangkil (efektif). Evaluasi yang dilakukan adalah CC meliputi pemeriksaan apakah seorang pengembang (1) mengikuti semua proses rekayasa perangkat lunak, dan (2) membuat produk yang aman dari serangan.

Pengembang CC di negara-negara lain dalpat dilihat pada tabel di bawah ini:

K-ISMS (Korea Information Security Management System), sebagai lingkungan yang menggunakan produk IT Security mendefinisikan bagaimana mengelola keamanan informasi dalam berbagai organisasi, baik organisasi berlaba atau nirlaba, swasta atau Pemerintah, kecil atau besar. K-ISMS mencakaup setiap aspek (fisik maupun logik) dari keamanan informasi, seperti peralatan, kebijakan manajemen, sumbersaya manusia, dan aspek hukum.

Semua yang saya ceritakan di atas menggambarkan betapa Korea sangat menaruh perhatian secara khusus terhadap bidang kriptografi di sana dan keamanan informasi pada umumnya. Mudaha-mudahan perkembangan kriptografi di Indonesia pun dapat mengikyi jejak Korea yang sudah sangat maju dalam bidang tersebut.

(Keterangan: semua gambar diambil dari presentasi dosen Korea University)

Proteksi Perangkat Lunak dengan Kriptografi dan Perangkat Keras

Wuaahh… sudah lama saya absen menulis di blog ini. Hari ini saya mulai lagi. Sebenarnya ini sudah agak telat, karena wisuda sarjana ITB sudah selesai. Kenapa wisuda? Karena yang saya bahas kali ini adalah Tugas Akhir mahasiswa saya di Informatika ITB.

Mahasiswa saya bernama Samudra Harapan Bekti, Informatika ITB Angkatan 2008, mengerjakan topik Tugas Akhir yang sangat menarik dan membuat saya angkat topi. Saya beri dia nilai A++ karena idenya orisinil dan hasilnya sangat bermanfaat buat industri perangkat lunak.

Dia mengangkat topik proteksi perangkat lunak dari penggandaan secara ilegal. Selama ini penggandaan perangkat lunak cukup sulit dicegah. Hal ini karena sifat data digital yang mudah digandakan. Memang sudah banyak dikembangkan orang proteksi berbasis perangkat lunak juga, tetapi tetap saja tidak berhasil menanggulangi masalah pembajakan.

Berangkat dari hobi dan ketertarikannya dengan elektronika sejak SMA, dia membuat sistem proteksi perangkat lunak berbasis perangkat keras. Idenya adalah perangkat keras sulit digandakan, dan inilah yang menjadi dasar sistem proteksinya itu.

Dia merancang sendiri pengendali mikro (microcontroller) untuk menyimpan kunci lisensi perangkat lunak. Perangkat lunak yang diproteksi dienkripsi terlebih dahulu dengan kunci tersebut. Perangkat lunak terenkripsi (misal disimpan di dalam CD atau DVD) didistribusikan (atau dijual) kepada konsumen bersama dengan pengendali mikro tadi. Sebuah antarmuka USB digunakan untuk menghubungkan perangkat keras dengan komputer pengguna. Di dalam CD/DVD terdapat perangkat lunak yang dienkripsi dan sebuah program loader yang diaktifkan pada waktu aktivasi produk pertama kali.

Ilustrasi: Contoh sebuah USB microcontroller (Sumber: https://www.olimex.com/dev/mod-mma7260q.html)

USB Microcontroller yang dirancang Samudra Harapan Bekti (Sumber: laman fesbuk ybs di http://www.facebook.com/photo.php?fbid=4008407243732&set=a.4008358162505.2163560.1087712270&type=3&theater)

Dikutip dari laporan TA Samudera Harapan Bekti, pengendali mikro adalah sistem komputer yang terintegrasi di dalam sebuah chip. Chip tersebut disusun oleh prosesor, memori, dan perangkat masukan/keluaran yang dapat diprogram untuk menjalankan fungsi tertentu. Pengendali mikro dapat dimanfaatkan sebagai bagian dari sistem proteksi perangkat lunak untuk menggantikan peran server aktivasi sehingga proses aktivasi perangkat lunak dapat dilakukan di luar jaringan (offline).

Saya tidak akan membahas mengenai rancangan pengendali mikronya, karena saya tidak punya keahlian disitu. Yang ingin saya bahas adalah penggunaan kriptografi di dalam sistem proteksi tersebut.

Perangkat lunak yang diproteksi dienkripsi dengan sebuah algoritma kriptografi (dia memakai algoritma AES) dan kunci rahasia. Kunci rahasia ditanam di dalam USB. Kunci akan dikirim oleh program loader ke komputer pengguna ketika pengguna melakukan aktivasi produk. Kunci dipakai untuk mendekripsi perangkat lunak yang telah dienkripsi.

Kunci yang dipakai untuk mengenkripsi perangkat lunak dienkripsi lagi dengan sebuah session key. Session key ini dihitung dengan algoritma kunci-publik Diffie-Hellman. Kunci privat (private key) yang digunakan di dalam algoritma Diffie-Hellman diambil dari ID hardware yang bersifat unik untuk setiap komputer, sedangkan kunci publiknya (public key) ditentukan oleh pengembang perangkat lunak dan disimpan di dalam USB microcontroller.

Ketika pengguna mengaktivasi produk, program loader meminta pengguna memasukkan USB ke komputer. Selanjutnya terjadi proses perhitungan session key dengan algoritma Diffie-Hellman dengan menggunakan kunci privat (ID hardware) dan kunci publik yang tersimpan di dalam USB tadi.

Session key mendekripsi kunci master, selanjutnya kunci master digunakan untuk mendekripsi perangkat lunak yang diproteksi.

Yang menarik adalah di dalam USB juga dapat disertakan jumlah lisensi yang memungkinkan pengguna menginstalasi produk pada lebih dari satu komputer. Setiap kali aktivasi maka lisensi berkurang satu. Selain itu aktivasi produk dilakukan satu kali saja, tetapi setiap kali menjalankan perangkat lunak program loader akan memeriksa validitas nilai tertentu yang disimpan di dalam sebauh berkas eksternal.

Saya berharap karya TA-nya ini dapat dikembangkan dan diproduksi secara massal untuk mencegah penggandaan ilegal. USB dapat dibuat secara massal di pabrik dengan sebuah kunci lisensi tertentu. Pengembang dapat menyimpan kunci lisensi di dalam USB dan menentukan jumlah lisensi yang dibeli. Perangkat lunak dijual dalam satu paket yang berisi CD/DVD program dan USB tersebut.

Enkripsi Selektif Citra Digital dalam Ranah Spasial

Saya sedang melakukan riset pengembangan beberapa algoritma enkripsi khusus untuk citra digital. Teknik enkripsi yang diinginkan adalah enkripsi selektif. Enkripsi selektif adalah mengenkripsi hanya sebagian elemen citra namun efeknya keseluruhan citra terenkripsi.  Di bawah ini saya paparkan sebuah teknik enkripsi selektif dalam ranah spasial.  Tulisan ini saya ambil sebagian dari makalah yang saya presentasikan di dalam konferensi SITIA 2012 di Kampus ITS Surabaya beberapa waktu yang lalu.

~~~~~~~~~~~~~~~~~~

1. PENDAHULUAN

Enkripsi citra bertujuan melindungi konten di dalam citra dari pengaksesan ilegal. Obyektif dari enkripsi citra adalah mentransformasikan citra ke dalam bentuk lain yang tidak bermakna sehingga konten di dalam citra tidak dapat dipahami lagi secara visual.

Mengenkripsi citra dengan algoritma enkripsi konvensional untuk data teks seperti DES, AES, Blowfish, dan lain-lain kurang cocok untuk aplikasi komunikasi yang real-time, sebab citra umumnya bervolume data sangat besar sehingga proses enkripsinya menjadi lambat. Oleh karena itu, solusi untuk masalah ini adalah dengan menggunakan konsep enkripsi selektif (atau sebagian) sebagai lawan dari enkripsi total [2]. Dengan teknik enkripsi selektif hanya sebagian komponen citra yang perlu dienkripsi namun sebagai efeknya citra dienkripsi secara keseluruhan. Tujuan enkripsi selektif jelas untuk meminimalkan volume komputasi selama proses enkripsi dan dekripsi.

Enkripsi selektif dapat dilakukan dalam ranah spasial atau dalam ranah frekuensi. Klasifikasi dan ringkasan beberapa algoritma enkripsi selektif dapat ditemukan di dalam [5], sedangkan performansi algoritmanya dapat dibaca di dalam [3].

Menurut [6], kebanyakan algoritma enkripsi citra dapat dikelompokkan menjadi dua golongan: (a) algoritma enkripsi selektif non-chaos, dan (b) algoritma enkripsi selektif atau non-selektif yang berbasis chaos. Chaos menjadi topik yang atraktif di dalam kriptografi karena tiga alasan: (1) sensitivitas terhadap kondisi awal, (2) berkelakuan acak, dan (3) tidak memiliki periode berulang. Penggunaan chaos di dalam kriptografi dapat menghasilkan efek confusion dan diffusion seperti yang disyaratkan oleh Shanon [8].

Kebanyakan skema enkripsi berbasis chaos menggunakan fungsi chaos (chaotic map) sebagai pembangkit barisan bilangan semi-acak (pseudo-random) yang panjang, kemudian barisan bilangan acak tersebut digunakan untuk mengenkripsi plainteks. Review beberapa algoritma enkripsi citra yang berbasis chaos dapat ditemukan di dalam [4].

Makalah ini membahas sebuah algoritma enkripsi selektif citra digital pada ranah spasial berbasis chaos. Sistematika makalah disusun menjadi tiga. Yang pertama adalah pendahuluan, bagian kedua adalah enkripsi selektif pada bit-bit MSB, dan bagian ketiga adalah eksperimen dan pembahasan hasil.

2. ENKRIPSI SELEKTIF PADA BIT-BIT MSB

Nilai pixel pada koordinat (x, y) menyatakan intensitas nilai keabuan pada posisi tersebut. Pada citra grayscale nilai keabuan itu dinyatakan dalam integer berukuran 1 byte sehingga rentang nilainya antara 0 sampai 255. Pada citra berwarna 24-bit setiap pixel tediri atas kanal red, green, dan blue (RGB) sehingga setiap pixel berukuran 3 byte (24 bit).

Di dalam setiap byte bit-bitnya tersusun dari kiri ke kanan dalam urutan yang kurang berarti (least significant bits atau LSB) hingga bit-bit yang berarti (most significant bits atau MSB).  Susunan bit pada setiap byte adalah b₇b₆b₅b₄b₃b₂b₁b₀. Jika setiap bit ke-i dari MSB ke LSB pada setiap pixel diekstrak dan diplot ke dalam setiap bitplane image maka diperoleh delapan buah citra biner. Misalnya bila dilakukan pada citra ‘cameraman’ (Gambar 1(a)) maka setiap bitplane image ditunjukkan pada Gambar 1(b) hingga 1(i). Gambar 1(b) hingga 1(f) yang diambil dari bit-bit MSB masih dapat memperlihatkan wujud objek di dalam citra sedangkan Gambar 1(g) hingga 1(i) yang diambil dari bit-bit LSB sudah terlihat seperti citra acak.

Gambar 1: Bitplane pada citra cameraman

Berdasarkan hasil ekstraksi bit-bit tersebut dapat disimpulkan bahwa pengubahan bit-bit MSB dapat membuat citra menjadi “rusak” atau tidak dapat dikenali lagi, sedangkan pengubahan bit-bit LSB tidak mempengaruhi citra secara keseluruhan. Oleh karena itu hanya bit-bit MSB saja yang dipilih untuk dienkripsi sebab dengan hanya mengenkripsi bit-bit tersebut maka keseluruhan citra menjadi tidak dapat dikenali lagi.

Jumlah bit MSB yang dienkripsi mempengaruhi tingkat keamanan. Jika hanya satu bit yang dienkripsi, maka tujuh bit sisanya (yang tidak ikut dienkripsi) masih dapat memperlihatkan wujud objek di dalam citra, sehingga tingkat keamanannya rendah. Oleh karena itu setelah enkripsi 1-bit MSB masih diperlukan prosedur permutasi tambahan untuk mengacak pixel agar diperoleh efek confusion [7].

Tao Xiang di dalam makalahnya menyebutkan bahkan enkripsi lebih dari dua bit MSB (tanpa prosedur pengacakan sesudahnya) masih tetap belum menjamin confidentiality citra. Untuk memperoleh keseimbangan antara tingkat keamanan dan pertimbangan performansi komputasi, maka enkripsi empat bit MSB (yaitu b₇b₆b₅b₄ )merupakan pemilihan yang optimal [1]. Dengan mengenkripsi hanya 4-bit MSB berarti cukup hanya dienkripsi 50% saja dari keseluruhan citra untuk memperoleh citra terenkripsi namun tingkat keamanannya tetap terjamin.

3. EKSPERIMEN DAN PEMBAHASAN HASIL

Setelah membahas teknik enkripsi selektif dalam ranah spasial, selanjutnya dilakukan implementasi algoritma tersebut. Algoritma enkripsinya seperti stream cipher namun enkripsi dilakukan per 4-bit setiap kali. Sebagai keystream generator adalah pembangkit bilangan acak berbasis chaos. Dalam hal ini, setiap 4-bit MSB dari setiap pixel di-XOR-kan dengan 4-bit keystream. Pada proses dekripsi, setiap 4-bit pixel dari cipher-image di-XOR-kan dengan 4-bit keystream. Untuk citra berwarna prosesnya dilakukan tiga kali, masing-masing untuk kanal red (R), green (G), dan blue (B).

Selanjutnya dilakukan simulasi enkripsi selektif pada citra uji, baik citra graysscale maupun citra berwarna. Dua buah citra standard yang digunakan adalah ‘Barbara’ (grayscale) dan ‘Lena’ (berwarna) yang keduanya berukuran 512 x 512 (Gambar 2), dan citra ketiga adalah ‘Taj Mahal’ yang berukuran 768 x 573.

Gambar 2. Tiga buah citra uji yang digunakan di dalam simulasi enkripsi dan dekripsi.

Citra hasil enkripsi (cipher-image) untuk ketiga citra uji di atas diperlihatkan pada Gambar 3. Citra hasil enkripsi terlihat sebagai citra acak dan sudah tidak bisa dikenali lagi. Dekripsi terhadap cipher-image menghasilkan kembali tepat seperti citra paad Gambar 1.

Gambar 3. Citra hasil enkripsi. Ketiga buah citra plain-image sudah tidak dapat dikenali lagi.

Analisis Histogram

Histogram merupakan properti citra yang penting sebab sebuah histogram memperlihatkan distribusi intensitas pixel di dalam citra tersebut. Untuk citra plain-image histogramnya membentuk suatu pola yang khas, yaitu ada puncak-puncak dan lembah-lembah. Untuk mencegah penyerang menggunakan histogram untuk melakukan analisis freluensi, maka histogram plain-image dan histogram cipher-image seharusnya tidak memiliki kemiripan secara statistik. Oleh karena itu, histogram cipher-image seharusnya relatif datar (flat) sehingga tahan terhadap serangan statistik. Distribusi yang relatif uniform pada cipher-image adalah sebuah indikasi bahwa algoritma enkripsi citra memiliki kualitas yang bagus [9].

Gambar 4(a) memperlihatkan histogram citra ‘Barbara’ sebelum dienkripsi, dan Gambar 4(b) adalah histogram cipher-image-nya. Dapat dilihat bahwa histogram cipher-image memiliki distribusi uniform yang mana berbeda dengan histogram plain-image.

Gambar 4. (a) Histogram citra ‘Barbara’ (plain-image) dan (b) histogram cipher-image.

Gambar 5(a) sampai 5(c) memperlihatkan histogram citra ‘Lena’ (plain-image) untuk setiap kanal warna RGB dan Gambar 5(d) sampai 5(f) adalah histogram masing-masang kanal warna pada cipher-image. Sama seperti citra ‘Barbara’, histogram cipher-image pada setiap kanal RGB juga terlihat flat atau terdistribusi uniform.

Gambar 5. (a)-(c) Histogram citra ‘Lena’ (plain-image) untuk masing-masing kanal RGB dan (d)-(f) histogram cipher-image untuk setiap kanal RGB.

Gambar 6(a) memperlihatkan histogram citra ‘Taj Mahal’ (plain-image) dan Gambar 8(b) adalah histogram cipher-image-nya. Sedikit berbeda dengan histogram cipher-image dari dua citra sebelumnya, histogram cipher-image dari ‘Taj Mahal’ memiliki distribusi yang relatif uniform.

Gambar 6 (a) Histogram citra ‘Taj Mahal’ (plain-image) dan (b) histogram cipher-image.

Berdasarkan hasil-hasil analisis histogram di atas dapat disimpulkan bahwa cipher-image memiliki histogram yang (relatif) flat sehingga menyulitkan penyerang melakukan analisis statistik untuk mendeduksi pixel atau kunci. Hasil ini menunjukkan bahwa algoritma enkripsi citra yang diusulkan ini memiliki keamanan yang bagus.

DAFTAR REFERENSI

[1] Tao Xiang, Kwok-wo Wong, Xiaofeng Liao, Selective Image Encryption Using a Spatiotemporal Chaotic System, Chaos Volume 17, 2007.
[2] Nidhi S Kulkarni, Balasubrmanian Raman, Indra Gupta, Selevtive Encryption of Multimedia Images, Proc. Of XXXII National Systems Conference, NSC 2008, December 17-19, 2008.
[3] Jolly Shah, Vikas Saxena, Performance Study on Image Encryption Schemes, International Journal of Computer Science Issues, Vol 8, Issue 4, No 1, July 2011.
[4] Monisha Sharma, Manoj Kumar Kowar, Image Encryption Techniques Using Chaotic Schemes: A Review, International Journal of Engineering Science and Technology, Vol. 2(6), 2010
[5] Xiliang Liu, Selective Encryption of Multimedia Contentn in Distribution Networks: Challenges and New Directions, Proc. of Conference of Communications, Internet, and Information Technology, 2003.
[6] Mohammad Ali Bani Younes, Aman Jantan, Image Encryption Using Block-based Transformation Algorithm, IAENG International Journal of Computer Science, 35: 1, IJCS_32_1_03, 2008.
[7] Rinaldi Munir, Enkripsi Selektif Citra Digital dengan Stream Cipher Berbasiskan pada Fungsi Chaotik Logistic Map, Seminar Nasional dan Expo Teknik Elektro Univeristas Syiah Kuala, Banda Aceh, Oktober 2011.
[8] Bruce Schneier, Applied Cryptography 2nd Edition, Wiley & Sons, 1996.
[9] Alireza Jolfaei, Abdul Rasoul Mirghadri, An Image Encryption Approach Using Chaos and Stream Cipher, Journal of Theoretical and Applied Information Technology, 2010.
[10] James Lampton, Chaos Cryptography: Protecting data Using Chaos, Missisippi School for Mathematics and Science.

Skema Pembagian Data Rahasia dari Shamir (Bagian 2)

Selain menggunakan metode eliminasi Gauss untuk menemukan solusi polinom interpolasi, metode lain yang dipakai untuk membentuk polinom secara langsung adalah dengan menggunakan metode interpolasi. Jika anda pernah mengambil kuliah metode numerik, anda tentu pernah mempelajari metode-metode meninterpolasi sejumlah titik data dengan polinom.

Salah satu metode interpolasi polinom adalah Polinom Lagrange. Misalkan diberikan t buah titik yaitu (x1, y1), (x2, y2), …, (xt, yt). Polinom Lagrange, dalam modulo p, yang melalui t titik adalah polinom derajat t– 1:

                                        p(x)  = y₁L1(x₁) + y₂L₂(x₂) + … + y_tL_t(x_t) (mod p),

yang dalam hal ini:

Polinom Lagrange ini harus dirahasiakan supaya pihak lawan tidak bisa menghitung secret M. Untuk memperoleh secret M caranya mudah, yaitu bila diketahui polinom p(x) maka hitung p(x) pada x = 0.

Misalkan partisipan 2, 3, dan 7 menggunakan interpolasi Lagrange, mereka mengumpulkan semua share mereka:
(x₁, y₁) = (2, 1045116192326)
(x₂, y₂) = (3, 154400023692)
(x₃, y₃) = (7, 973441680328)

Mereka kemudian membentuk polinom Lagrange derajat dua:p(x) = y₁L₁(x₁) + y₂L₂(x₂) + y₃L₃(x₃) (mod p), dan diperoleh hasilnya sebagai berikut:

p(x) =  20705602144728/5 – 1986192751427x + (1095476582793/5)x² (mod p)

Karena polinom  dihitung dalam modulus p dan dengan mengingat 740740734080  dikali 5 kongruen dengan 1 (mod p), maka 1/5 dapat diganti dengan 740740734080, sehingga kita memperoleh polinom tanpa modulo p:

p(x) = 190503180520 + 482943028839x +120674920705602144728x²

Untuk memproleh M, hitung p(0), dan diperoleh p(0) = 190503180520 = M, yaitu secret semula.

 

Referensi

1. Trappe, W., Washington, L. (2006): Introduction to Cryptography with Coding Theory, Prentice Hall.